Trung tâm đào tạo thiết kế vi mạch Semicon

Login

Username: Password:

Forgot your password? Forgot your username?
ĐĂNG KÝ TÀI KHOẢN ĐỂ TRUY CẬP NHIỀU TÀI LIỆU HƠN!

Create an account

Skip to content

Digital Number System Part-II

Thursday, 23 December 2021 16:08 Semicon Editor 01

Code Conversion

Converting from one code form to another code form is called code conversion, like converting from binary to decimal or converting from hexadecimal to decimal.

Binary-To-Decimal Conversion
Any binary number can be converted to its decimal equivalent simply by summing together the weights of the various positions in the binary number which contain a 1.

Binary	Decimal
11011₂	Â
2⁴+2³+0¹+2¹+2⁰	=16+8+0+2+1
Result	27₁₀

and

Binary	Decimal
10110101₂	Â
2⁷+0⁶+2⁵+2⁴+0³+2²+0¹+2⁰	=128+0+32+16+0+4+0+1
Result	181₁₀

You should have noticed that the method is to find the weights (i.e., powers of 2) for each bit position that contains a 1, and then to add them up.

Decimal-To-Binary Conversion
There are 2 methods:

Reverse of Binary-To-Decimal Method
Repeat Division

Reverse of Binary-To-Decimal Method

Decimal	Binary
45₁₀	=32 + 0 + 8 + 4 +0 + 1
Â	=2⁵+0+2³+2²+0+2⁰
Result	=101101₂

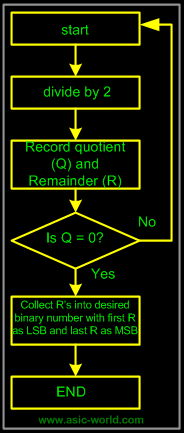
Repeat Division-Convert decimal to binary
This method uses repeated division by 2.

Convert 25₁₀ to binary

Division	Remainder	Binary
25/2	= 12+ remainder of 1	1 (Least Significant Bit)
12/2	= 6 + remainder of 0	0
6/2	= 3 + remainder of 0	0
3/2	= 1 + remainder of 1	1
1/2	= 0 + remainder of 1	1 (Most Significant Bit)
Result	25₁₀	= 11001₂

The Flow chart for repeated-division method is as follows:

Binary-To-Octal / Octal-To-Binary Conversion

Octal Digit	0	1	2	3	4	5	6	7
Binary Equivalent	000	001	010	011	100	101	110	111

Each Octal digit is represented by three binary digits

Â

Example

100 111 010₂ = (100) (111) (010)₂ = 4 7 2₈

Repeat Division-Convert decimal to octal
This method uses repeated division by 8.
Example: Convert 177₁₀ to octal and binary

Division	Result	Binary
177/8	= 22+ remainder of 1	1 (Least Significant Bit)
22/ 8	= 2 + remainder of 6	6
2 / 8	= 0 + remainder of 2	2 (Most Significant Bit)
Result	177₁₀	= 261₈
Binary	Â	= 010110001₂

Hexadecimal to Decimal/Decimal to Hexadecimal Conversion
Example:
2AF₁₆ = 2 x (16²) + 10 x (16¹) + 15 x (16⁰) = 687₁₀

Repeat Division- Convert decimal to hexadecimal
This method uses repeated division by 16.

Example: convert 378₁₀ to hexadecimal and binary:

Division	Result	Hexadecimal
378/16	= 23+ remainder of 10	A (Least Significant Bit)23
23/16	= 1 + remainder of 7	7
1/16	= 0 + remainder of 1	1 (Most Significant Bit)
Result	378₁₀	= 17A₁₆
Binary	Â	= 0001 0111 1010₂

Binary-To-Hexadecimal /Hexadecimal-To-Binary Conversion

Hexadecimal Digit

0

1

2

3

4

5

6

7

Â

Binary Equivalent

0000

0001

0010

0011

0100

0101

0110

0111

Â

Hexadecimal Digit	8	9	A	B	C	D	E	F
Binary Equivalent	1000	1001	1010	1011	1100	1101	1110	1111

Each Hexadecimal digit is represented by four bits of binary digit.

Example:

1011 0010 1111₂ = (1011) (0010) (1111)₂ = B 2 F₁₆

Octal-To-Hexadecimal Hexadecimal-To-Octal Conversion

Convert Octal (Hexadecimal) to Binary first.
Regroup the binary number by three bits per group starting from LSB if Octal is required.
Regroup the binary number by four bits per group starting from LSB if Hexadecimal is required.
Example:
Convert 5A8₁₆ to Octal.