Introduction
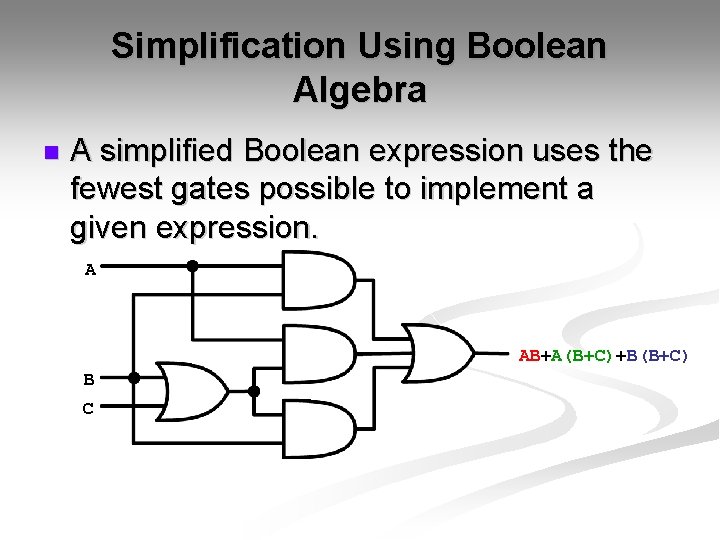
Simplification of Boolean functions is mainly used to reduce the gate count of a design. Less number of gates means less power consumption, sometimes the circuit works faster and also when number of gates is reduced, cost also comes down.
There are many ways to simplify a logic design, some of them are given below. We will be looking at each of these in detail in the next few pages.
- Algebraic Simplification.
- Simplify symbolically using theorems/postulates.
- Requires good skills
- Karnaugh Maps.
- Diagrammatic technique using 'Venn-like diagram'.
- Limited to no more than 6 variables.
We have already seen how Algebraic Simplification works, so lets concentrate on Karnaugh Maps or simply k-maps.
Karnaugh Maps
Karnaugh maps provide a systematic method to obtain simplified sum-of-products (SOPs) Boolean expressions. This is a compact way of representing a truth table and is a technique that is used to simplify logic expressions. It is ideally suited for four or less variables, becoming cumbersome for five or more variables. Each square represents either a minterm or maxterm. A K-map of n variables will have 2
squares. For a Boolean expression, product terms are denoted by 1's, while sum terms are denoted by 0's - but 0's are often left blank.
A K-map consists of a grid of squares, each square representing one canonical minterm combination of the variables or their inverse. The map is arranged so that squares representing minterms which differ by only one variable are adjacent both vertically and horizontally. Therefore XY'Z' would be adjacent to X'Y'Z' and would also adjacent to XY'Z and XYZ'.
Minimization Technique
- Based on the Unifying Theorem: X + X' = 1
- The expression to be minimized should generally be in sum-of-product form (If necessary, the conversion process is applied to create the sum-of-product form).
- The function is mapped onto the K-map by marking a 1 in those squares corresponding to the terms in the expression to be simplified (The other squares may be filled with 0's).
- Pairs of 1's on the map which are adjacent are combined using the theorem Y(X+X') = Y where Y is any Boolean expression (If two pairs are also adjacent, then these can also be combined using the same theorem).
- The minimization procedure consists of recognizing those pairs and multiple pairs.
- These are circled indicating reduced terms.
- Groups which can be circled are those which have two (21) 1's, four (22) 1's, eight (23) 1's, and so on.
- Note that because squares on one edge of the map are considered adjacent to those on the opposite edge, group can be formed with these squares.
- Groups are allowed to overlap.
- The objective is to cover all the 1's on the map in the fewest number of groups and to create the largest groups to do this.
- Once all possible groups have been formed, the corresponding terms are identified.
- A group of two 1's eliminates one variable from the original minterm.
- A group of four 1's eliminates two variables from the original minterm.
- A group of eight 1's eliminates three variables from the original minterm, and so on.
- The variables eliminated are those which are different in the original minterms of the group.
Bạn Có Đam Mê Với Vi Mạch hay Nhúng - Bạn Muốn Trau Dồi Thêm Kĩ Năng
Mong Muốn Có Thêm Cơ Hội Trong Công Việc
Và Trở Thành Một Người Có Giá Trị Hơn
Bạn Chưa Biết Phương Thức Nào Nhanh Chóng Để Đạt Được Chúng
Hãy Để Chúng Tôi Hỗ Trợ Cho Bạn. SEMICON

